2.1 Bruchzahlen

Jeder Anteil kann durch verschiedene Brüche dargestellt werden. So ist z.B.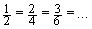

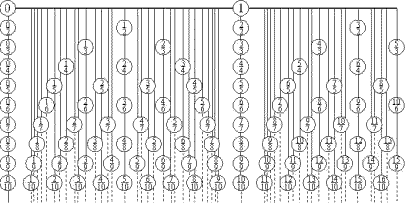
Jede Zahl kann durch verschiedene Brüche dargestellt werden. ℚ ist die Menge der Brüche. Es gilt: ℕ ⊂ ℤ ⊂ ℚ.

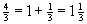
Brüche größer als 1 lassen sich auch durch gemischte Zahlen darstellen. Zwischen Ganzer Zahl und Bruch steht ein Additionszeichen.

Umwandlung gemischte Zahl in unechten Bruch:

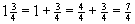
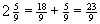
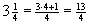
Multipliziere die Ganzen mit dem Nenner und addiere den Zähler. Dies ist der neue Zähler; behalte den Nenner bei.

Umwandlung Bruch in gemischte Zahl:

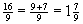
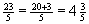
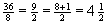
Subtrahiere vom Zähler ein Vielfaches des Nenners und schreibe das Vielfache als Ganze Zahl vor den Bruch. Der Rest ist der neue Zähler; behalte den Nenner bei.

2.2 Vergleich von Brüchen

1. gleiche Nenner: Der Bruch mit dem größeren Zähler ist größer. ,
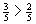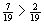
2. gleiche Zähler: Der Bruch mit dem größeren Nenner ist kleiner. ,
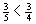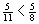
3. verschiedene Zähler und Nenner: Mittels Erweitern und Kürzen müssen die Brüche auf gleiche Zähler oder Nenner gebracht werden. ,

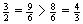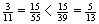
Ordne folgende Zahlen der Größe nach:

• →
• →
• →
• →

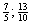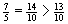
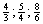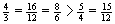
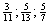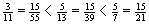
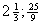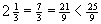
2.3 Rationale Zahlen

Alle positiven und negativen Brüche bilden zusammen die Menge der Rationalen Zahlen ℚ

Der Betrag einer Zahl ist ihr Abstand zur null.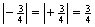

, , , ,
, ,

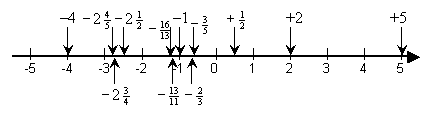
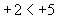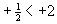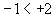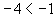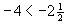
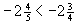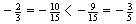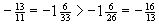
Bei der Anordnung negativer Zahlen ist die weiter rechts stehende Zahl größer, also die betragsmäßig kleinere Zahl.

Jede rationale Zahl q kann als Quotient einer ganzen Zahl z und einer natürlichen Zahl n dargestellt werden.

Für alle q ∈ ℚ gilt: 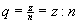mit z ∈ ℤ und n ∈ ℕ