4.1 Scheitelwinkel und Nebenwinkel

Winkel mit gemeinsamen Schenkel 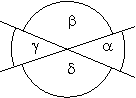an einer Geradenkreuzung bezeichnet man als Nebenwinkel, gegenüberliegende Winkel heißen Scheitelwinkel.

Scheitelwinkel sind punktsymmetrisch zum Geradenschnittpunkt und daher gleich groß, Nebenwinkel ergänzen sich zu einem gestreckten Winkel, also zu 180°.

Es gilt daher: α = γ und β = δ, sowie α + β = 180°, β + γ = 180°, &gamma + δ = 180° und α + δ = 180°.

4.2 Stufenwinkel und Wechselwinkel

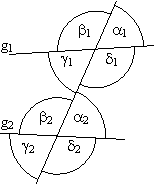Werden zwei nicht notwendig parallele Geraden g₁ und g₂ von einer dritten geschnitten, so nennt man gleichliegende Winkel β₁ & β₂ Stufenwinkel (F-Winkel). Winkel mit paarweise etwa entgegen gerichteten Schenkeln γ₁ & α₂ heißen Wechselwinkel (Z-Winkel). Entgegengesetzt liegende Winkel δ₁ & α₂ bezeichnet man Nachbarwinkel (E-Winkel).

Stufenwinkel und Wechselwinkel an geschnittenen Parallelen sind gleich groß, also α₁ = α₂, etc. falls g₁||g₂. Nachbarwinkel an geschnittenen Parallelen ergänzen sich zu 180°, also γ₁ + β₂ = 180°, α₁ + δ₂ = 180°, etc. falls g₁||g₂.

Die Gleichheit der Wechselwinkel an Parallelen folgt aus der Punktsymmetrie der Wechselwinkel zum Mittelpunkt der Verbindungsstrecke beider Geradenkreuzungen. Die Scheitelwinkel liefern dann die Gleichheit der Stufenwinkel. Mit den Nebenwinkeln folgt dann: Nachbarwinkel sind supplementär.

4.3 Innenwinkelsumme im Dreieck

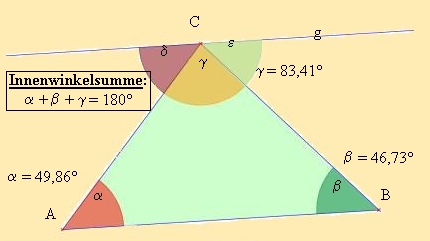
Errichtet man eine Parallele g zu AB durch den Punkt C, so gilt δ + γ + ε = 180°. Da in jedem beliebigen Dreieck aufgrund der Wechselwinkel an Parallelen
α = δ und β = ε gilt, folgt damit die Aussage: α + β + γ = 180° Innenwinkelsumme im Dreieck.

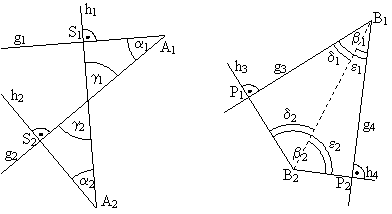Satz: Stehen die Schenkel zweier Winkel α₁ & α₂ bzw. β₁ & β₂ paarweise senkrecht aufeinander, so sind sie gleich groß α₁ = α₂,
oder supplementär β₁ + β_{2 = 180°.}

Beweis: Es gilt α₁ + γ₁ + 90° = 180° und α₂ + γ₂ + 90° = 180° (WS). Mit γ₁ = γ₂ (Scheitelwinkel) folgt dann: α₁ = α₂.

Es gilt δ₁ + δ₂ + 90° = 180° und ε₁ + ε₂ + 90° = 180° (WS) also δ₁ + ε₁ + δ₂ + ε₂ =β₁ + β₂ = 180°. q.e.d.

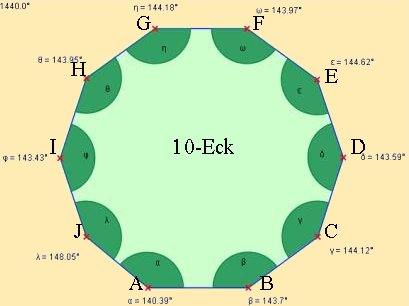
4.4 Innenwinkelsumme im Vieleck

Ein Viereck lässt sich in 2 Dreiecke zerlegen,
ein Fünfeck lässt sich in 3 Dreiecke zerlegen,
ein Achteck lässt sich in 6 Dreiecke zerlegen,
ein n-Eck lässt sich in (n-2) Dreiecke zerlegen.

Daher muss die Innenwinkelsumme des n-Ecks gleich der Innenwinkelsumme aller Zerlegungsdreiecke sein.

Innenwinkelsumme: