2. Die Quadratwurzel
2.1 Definition
Die positive Lösung der Gleichung ![]() bezeichnet man als Quadratwurzel aus a, kurz: Wurzel a. Man schreibt dafür
bezeichnet man als Quadratwurzel aus a, kurz: Wurzel a. Man schreibt dafür ![]() .
.
Die Zahl a unter der Wurzel bezeichnet man Radikand. Es gilt: ![]() , sowie
, sowie ![]()
Das Radizieren ist die Umkehrung des Quadrierens.
Es gilt: ![]() <=>
<=> ![]() bzw.
bzw. ![]() .
.
Ist der Radikand eine Summe, so lässt sich der Term nur vereinfachen, falls die Summe als Quadrat geschrieben werden. Der Summenterm heißt dann vollständiges Quadrat.
2.2 Irrationale Quadratwurzeln
|
Die Griechen entdeckten die Existenz irrationaler Zahlen am Problem der Quadratverdoppelung: „Wie lange ist die Seitenlänge eines Quadrats mit Flächeninhalt 2?“ Es gibt eine Strecke, deren Länge durch keine rationale Zahl angegeben werden kann. |
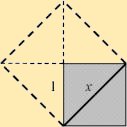 |
Die Menge der rationalen Zahlen ![]() ist unvollständig, da nicht für jede Streckenlänge eine rationale Maßzahl existiert.
ist unvollständig, da nicht für jede Streckenlänge eine rationale Maßzahl existiert.
|
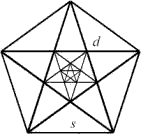
Das Teilungsverhältnis der Diagonalen eines regelmäßigen Fünfecks zur Grundseite ist ebenfalls irrational. Es trägt den Namen »Goldener Schnitt« und wird uns später in der Geometrie beschäftigen . Beweis zur Irrationalität von |
 |
Annahme: ![]() .
.
Sei ![]() mit
mit ![]() teilerfremd. Dann gilt:
teilerfremd. Dann gilt: ![]() also
also ![]() . Somit ist p2 gerade , also auch p gerade , da
. Somit ist p2 gerade , also auch p gerade , da ![]() . Es gilt daher:
. Es gilt daher: ![]() mit
mit ![]() und
und ![]() . Weil
. Weil ![]() ist ebenfalls q2 gerade , also auch q gerade , da
ist ebenfalls q2 gerade , also auch q gerade , da ![]() . Da p und q gerade sind, ist
. Da p und q gerade sind, ist ![]() . Dies ist ein Widerspruch zu p und q teilerfremd, also
. Dies ist ein Widerspruch zu p und q teilerfremd, also ![]() . q.e.d.
. q.e.d.
2.3 Berechnung von Quadratwurzeln
· Irrationale Punkte auf der Zahlengerade
Durch Abtragen der Diagonale des Einheitsquadrats lässt sich auf der Zahlengeraden ein Punkt P finden, dem keine rationale Zahl zugeordnet ist. Wir nennen diesen Punkt einen nicht rationalen oder irrationalen Punkt.

Auf der Zahlengeraden gibt es unendlich viele irrationale Punkte – sogar viel mehr als rationale Punkte.
· Intervallschachtelung
Durch systematisches Probieren finden wir ![]() :
:
|
Da |
liegt P im Intervall |
der Länge |
|
12 < 2 < 22 |
[1; 2] |
1 |
|
1,42 < 2 < 1,52 |
[1,4; 1,5] |
0,1 |
|
1,412 < 2 < 1,422 |
[1,41; 1,42] |
0,01 |
|
1,4142 < 2 < 1,4152 |
[1,414; 1,415] |
0,001 |
|
1,41422 < 2 < 1,41432 |
[1,4142; 1,4143] |
0,0001 |
|
1,414212 < 2 < 1,414222 |
[1,41421; 1,41422] |
0,00001 |
|
M |
M |
L M |
Unser Vorgehen wird an der Zahlengeraden besonders deutlich:
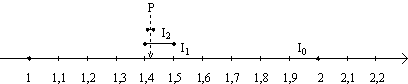
Wir erhalten eine Folge von Intervallen:
I0 = [1; 2]; I1 = [1,4; 1,5]; I2 = [1,41; 1,42]; …
Eine Folge I0, I1, I2, …, In, … von unendlich vielen Intervallen heißt Intervallschachtelung, wenn
1. jedes Intervall im vorangehenden vollständig enthalten ist und
2. die Länge der Intervalle mit wachsendem n beliebig klein wird.
· Das Heron-Verfahren
Nach Wahl eines Startwertes x0 liefert die Iterationsformel
![]() immer bessere Näherungswerte x1, x2, … für
immer bessere Näherungswerte x1, x2, … für ![]() . xn weicht vom exakten Wert für
. xn weicht vom exakten Wert für ![]() um weniger als
um weniger als ![]() ab.
ab.
2.4 Die Menge der reellen Zahlen 
Die rationalen Zahlen und die irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen ![]() .
.
Die rationalen Zahlen lassen sich durch endliche oder unendliche periodische Dezimalbrüche darstellen.
Zahlen, die sich durch unendliche nichtperiodische Dezimalbrüche darstellen lassen, heißen irrationale Zahlen.
Rationale Zahlen: ![]()
![]()
![]()
![]()
Irrationale Zahlen: 0,12 122 1222 12222 … ![]() 0,23456789 2022232425… 0,785453896247986923565885…
0,23456789 2022232425… 0,785453896247986923565885…
![]()
![]()
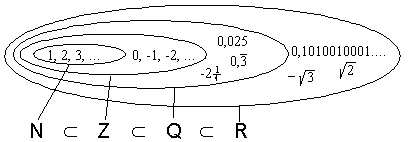
2.5 Der Körper der reellen Zahlen
|
Addition |
Multiplikation |
|
|
(E) Sind |
|
|
|
(K) Für alle |
|
|
|
(A) Für alle |
|
|
|
(N) In mit der Eigenschaft |
neutrale Element 0
|
neutrale Element 1
|
|
(I) Für jedes mit der Eigenschaft |
ein inverses Element – a
|
ein inverses Element
|
|
(D) Für alle |
|
|
Ordnungsaxiom: Für ![]() gilt:
gilt: ![]() oder
oder ![]() oder
oder ![]() .
.
(O1) Wenn ![]() und
und ![]() , dann ist
, dann ist ![]() .
.
(O2) Wenn ![]() , dann
, dann ![]() .
.
(O3) Wenn ![]() und
und ![]() , dann ist
, dann ist ![]() .
.
Vollständigkeitsaxiom:
Jedem Punkt der Zahlengerade lässt sich eine Zahl zuordnen.
![]() ist kein Körper.
ist kein Körper.
![]() ist ein geordneter Körper, aber nicht vollständig.
ist ein geordneter Körper, aber nicht vollständig.
![]() ist ein vollständig geordneter Körper.
ist ein vollständig geordneter Körper.
2.6 Rechenregeln für Wurzeln
Multiplikationsregel:
Für beliebige Zahlen ![]() gilt:
gilt: ![]()
![]()
allgemein: Für ![]() gilt:
gilt: ![]() .
.
Divisionsregel:
Für beliebige Zahlen ![]() und
und ![]() gilt:
gilt: ![]()
allgemein: Für ![]() und
und ![]() \
\ ![]() gilt:
gilt: ![]() .
.
![]() lässt sich im allgemeinen nicht vereinfachen.
lässt sich im allgemeinen nicht vereinfachen.
Summen und Differenzen lassen sich nur mit Hilfe des Distributivgesetzes zusammenfassen.
Einen rationalen Nenner erreicht man durch Erweitern mit einem Wurzelwert oder mit einer irrationalen Summe unter Anwendung der dritten binomischen Formel.
![]()
![]()
Zu jedem Radikanden ![]() gibt es genau einen Wurzelwert
gibt es genau einen Wurzelwert ![]() . Deshalb gilt:
. Deshalb gilt:
Zwei Quadratwurzeln ![]() und
und ![]() sind genau dann gleich, wenn ihre Radikanden a und b gleich sind.
sind genau dann gleich, wenn ihre Radikanden a und b gleich sind.
![]() <=>
<=> ![]()
Du möchtest mehr?
Nachhilfe
Du schreibst bald einen Test, verstehst ein bestimmtes Thema aber noch nicht oder du brauchst einfach nur Hilfe bei den Hausaufgaben?
Du kannst mich gerne jederzeit kontaktieren, damit wir einen Termin ausmachen können.
Coaching
Prozent- und Zinsrechnungen sind nicht so dein Ding?
Ich kann dir dabei helfen, altes Wissen wieder aufzufrischen.
Du kannst mich gerne jederzeit kontaktieren, damit wir einen Termin ausmachen können.
