4. Lineare Gleichungssysteme

4.1 Lineare Gleichungen mit zwei Variablen

Eine Gleichung ,   und  ,  heißt implizite lineare Gleichung mit zwei Variablen. Ihre Lösungsmenge   enthält unendliche viele Zahlenpaare als Lösung. Die graphische Darstellung der Lösungsmenge ist eine Gerade.

 heißt auch explizite Form der Gleichung.

Für &  erhält man , eine Parallele zur x-Achse,
für &  erhält man , eine Parallele zur y-Achse.

4.2 Lineares Gleichungssystem mit zwei Variablen

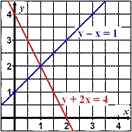
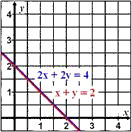
Zwei lineare Gleichungen mit zwei gemeinsamen Variablen (I)  und  (II)  bilden ein lineares Gleichungssystem mit zwei Variablen. Ein Zahlenpaar (x|y)² heißt Lösung, wenn es beide Gleichungen des Gleichungssystems erfüllt.

Ein Gleichungssystem lässt sich lösen, indem man z.B. die expliziten Formen beider Gleichungen gleich setzt. Man erhält:

• genau eine Lösung, den Schnittpunkt beider Geraden,
• keine Lösung; die Geraden sind parallel,
• unendlich viele Lösungen; die Geraden sind identisch.

4.3 Einsetzverfahren

1. Auflösen einer Gleichung nach einer Variablen liefert eine Zuordnung der beiden Variablen.
2. Setzt man diese in die andere Gleichung auf, lässt sich der Wert einer Variablen bestimmen.
3. Einsetzen in eine Gleichung mit zwei Variablen liefert den anderen Variablenwert.
4. Die Lösung ist das Zahlenpaar beider Variablen.

4.4 Additionsverfahren

1. Multipliziere beide Gleichungen mit Faktoren so, dass eine Variable in beiden Gleichungen betragsgleiche Koeffizienten hat.
2. Addieren bzw. Subtrahieren liefert eine Gleichung mit einer Variablen, die nun bestimmt werden kann.
3. Einsetzen in eine Gleichung mit zwei Variablen liefert den anderen Variablenwert.
4. Die Lösung ist das Zahlenpaar beider Variablen.

4.5 Anwendungssituationen

1. Definition bzw. Einführung der Variablen
2. Gleichungssystem aufstellen
3. Gleichungssystem lösen
4. Antwort mit sinnvoller Lösung angeben

4.6 Lineare Gleichungssysteme mit drei Variablen

1. Zwei Gleichungen mit den selben Variablen ermitteln
2. Eine Gleichung mit einer Variablen ermitteln
3. Nach der ersten Variablen auflösen und in eine Gleichung mit zwei Variablen einsetzen
4. Nach der zweiten Variablen auflösen und beide in eine Gleichung mit drei Variablen einsetzen
5. Nach der dritten Variablen auflösen
6. Sinnvolle Antwort formulieren