5. Laplace-Wahrscheinlichkeit

5.1 Grundbegriffe

Ein Zufallsexperiment ist das Herbeiführen einer Entscheidung, die nicht beeinflusst werden kann, also zufällig erfolgt.
Beispiele hierfür sind: Würfeln, Münzwurf, Drehen eines Glücksrades, Ziehen aus einer Urne, Kartenziehen, etc.

Bei der Durchführung von Zufallsexperimenten tritt stets genau ein Ergebnis auf. Diese werden mit ω 1, ω 2, ω 3, … bezeichnet. Die Menge aller möglichen Ergebnisse heißt Ergebnismenge . Ein Ereignis tritt ein, wenn ein Ergebnis ω  A einer Teilmenge A der Ergebnismenge Ω, kurz A Ω, eintritt.

Das Ereignis Ω tritt immer ein und heißt sicheres Ereignis. Das Ereignis Ø tritt nie ein und heißt unmögliches Ereignis. Das Gegenereignis  enthält alle Ergebnisse , für die gilt: . Man schreibt auch \ A. Es gilt: . Man nennt A und  komplementär. Zwei Ereignisse A und B heißen disjunkt, wenn sie kein gemeinsames Ergebnis haben, kurz: .

5.2 Relative Häufigkeit und Wahrscheinlichkeit

Für n Versuche gilt damit für Ereignis A = {ω 1 +ω 2 +…+ ω k }:
H (A) = H(ω 1 ) + H(ω 2 ) + … + H( ω k )

h (A) = h(ω 1 ) + h(ω 2 ) + … + h( ω k ) = H(A) : n

Bei einem Zufallsexperiment wird jedem Ergebnis ω_i eine Wahrscheinlichkeit 0 < P(ω_i) ≤ 1 zugeordnet. Der Wert ist körper- und formbedingt und gibt den Anteil des Auftretens an der Gesamtzahl der Versuche an.

Empirisches Gesetz der großen Zahlen:

Bei einem Zufallsexperiment tritt jedes Ergebnis ωi mit einer Wahrscheinlichkeit P(ωi) auf. Mit steigender Versuchsanzahl stabilisiert sich die relative Häufigkeit der Ergebnisse h(ωi) und nähert sich der Wahrscheinlichkeit an:

Für die Wahrscheinlichkeit von Ereignissen betrachtet man die Ergebnisse als Elementarereignisse. Man definiert intuitiv:

P(Ø) = 0 und P(Ω) = 1 .

Additionsgesetz der Wahrscheinlichkeitsrechnung:

, falls  paarweise disjunkt für alle .

Beeinflusst das Auftreten eines Ereignisses A das Auftreten des Ereignisses B nicht, so nennt man A und B unabhängig.

Multiplikationsgesetz der Wahrscheinlichkeitsrechnung:

, falls  paarweise unabhängig für alle .

5.3 Laplace-Experimente

Haben bei einem Zufallsexperiment alle Ergebnisse die gleiche Wahrscheinlichkeit, so nennt man es Laplace-Experiment. Gibt es k Ergebnisse, so gilt:  für alle .

Für die Anzahl der Elemente einer Menge A schreibt man |A|. Bei Ereignissen spricht man auch von Mächtigkeit.

Für die Wahrscheinlichkeit eines Ereignisses A gilt beim Laplace-Experiment: . Damit gilt: .

5.4 Mehrstufige Laplace-Experimente

Zur Veranschaulichung bietet sich ein Baumdiagramm an.

Bsp. dreimaliges Werfen einer Münze

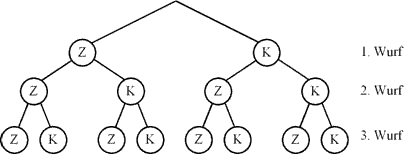
Es gilt: 

Für die Bestimmung der Gesamtzahl an Ergebnissen bei mehrstufigen Zufallsexperimenten verwendet man folgendes Zählverfahren: Zieht man aus kverschiedenen Mengen mit m 1, m 2, … m k Elementen jeweils ein Element, so gibt es insgesamt  Möglichkeiten.

Für den dreifachen Münzwurf gilt damit 

Es gilt: Ereignis 

und Ereignis , also  und 

»Ziehen mit Zurücklegen« bezeichnet ein Zufallsexperiment, bei dem stets die gleiche Ergebnismenge zugrunde liegt.
»Ziehen ohne Zurücklegen« bezeichnet ein Zufallsexperiment, bei dem jedes Ergebnis nur einmal ausgewählt werden kann.

Bsp. dreimaliges Werfen eines Würfels

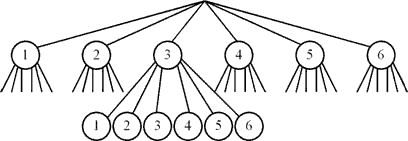
Bsp. 4 Schüler setzen sich beliebig auf 4 Plätze

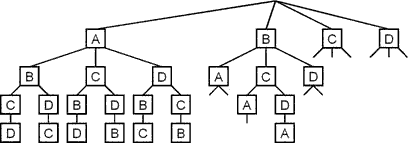
Schreibweise: , sprich n Fakultät

Das n-fache Auswählen aus k Objekten hat k ⁿ Möglichkeiten, das Anordnen von k Objekten hat k ! Möglichkeiten.

5.5 Modellieren realer Situationen

Man sucht ein möglichst einfaches Zufallsexperiment mit der Wahrscheinlichkeitsverteilung der Situation. Nun ordnet man jedem Ergebnis eine Entscheidung der realen Situation zu.