2.1 Der Funktionsbegriff

Eine Funktion ist die eindeutige Zuordnung einer Variablen x zu einer Größe y. Die Definitionsmenge legt die Variablen fest, die Wertemenge vereinigt die zugeordneten Größen . Die Zuordnung wird durch die Funktionsvorschrift festgelegt. Die zusammengehörigen Paare  stellen den Graph G f der Funktion dar. Kurz schreibt man dafür: ,

 

2.2 Der Kreisumfang

Um den Tacho eines Fahrrades zu justieren, muss man den Umfang des Reifens eingeben. Wie kann man den Umfang bei gegebener Reifengröße 28″ (26″, 24″) ermitteln?

Vorüberlegung:

Da die Größe des Kreises durch den Durchmesser eindeutig festgelegt wird, muss auch der Umfang vom Durchmesser abhängen.

Ein Vergleich der Dimensionen legt die Vermutung nahe.

Abschätzung des Umfangs:

Der Umfang des Kreises U_K ist kleiner als der Umfang U_Q des umschriebenen Quadrates und größer als der Umfang U_6-Eck des einbeschriebenen 6-Ecks. Damit gilt: .

Bestimmung der Konstanten c:

Von mehreren zylindrischen Gegenständen wird der Umfang U_K und der Durchmesser d der Grundfläche gemessen.

Durchmesser d in cm
Umfang UK in cm
Konstante

Als Mittelwert für die Konstante c ergibt sich:

Die Zahl p wird als transzendent bezeichnet und es gilt pÏ?. Darunter versteht man eine unendlich nicht periodische Zahl, deren Größe nicht durch Konstruktion ermittelt werden kann.

Für die Kreisbogenlänge b eines Kreissektors mit Radius r und Mittelpunktswinkel m gilt: , also

2.3 Der Flächeninhalt des Kreises

In einer Pizzeria gibt es kleine Pizzen mit Durchmesser
d_kl = 20 cm und große Pizzen mit Durchmesser. d_gr = 24 cm.
Um wie viel ist nun die große Pizza größer als die kleine?

Vorüberlegung:

Da die Größe des Kreises durch den Radius eindeutig festgelegt wird, muss auch der Flächeninhalt vom Radius abhängen.

Ein Vergleich der Dimensionen legt die Vermutung nahe.

Abschätzung des Flächeninhalts:

Der Flächeninhalt des Kreises A_K liegt zwischen den Flächeninhalten A_Q1 und A_Q2 der beiden Quadrate. Damit gilt: .

Bestimmung der Konstanten c:

Unterteilt man einen Kreis in 12 Kreissektoren und ordnet diese wie Kuchenstücke beim Konditor zu einer Art Rechteck, so erhält man folgendes:

Die Kreisfläche ist damit gleich dem Flächeninhalt des Rechtecks, also und somit .

Erhöht man die Anzahl der Kreissektoren, so nähert sich die „gewellte“ Figur immer besser einem Rechteck.

Fläche eines Kreissektors:

, also

Fläche eines Kreissegments:

mit

mit Mittelpunktswinkel m und Radius r

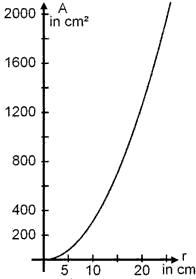
Die Fläche des Kreises lässt sich auch als Funktion vom Radius auffassen:
A : ?⁺ ® ?⁺, .

Eine solche Funktion nennt man Quadratische Funktion, da die Variable, hier r, im Quadrat auftritt.

Der Graph dieser Funktion ist eine Parabel.

 

so sollte es sein:

Fläche eines Kreissegments

 mit 

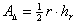
mit Mittelpunktswinkel µ und Radius r

Die Fläche des Kreises lässt sich auch als Funktion vom Radius auffassen:
, .

Eine solche Funktion nennt man Quadratische Funktion, da die Variable, hier r, im Quadrat auftritt.

Der Graph dieser Funktion ist eine Parabel.